I am a postdoctoral scholar at UC Berkeley working with Prof. Kannan Ramchandran. Before this, I spent six wonderful years at UT Austin advised by Prof. Alex Dimakis, and have been lucky to collaborate with Prof. Eric Price on several projects. I received my B.Tech. (Honors) in Electrical Engineering from IIT Madras in 2016, where I worked closely with Prof. Rahul Vaze, Prof. Umang Bhaskar, and Prof. Krishna Jagannathan.
My research interests lie at the intersection of theory and practice. I design and analyze algorithms that use deep generative models in inverse problems and other related areas of signal processing. On the theoretical side, my work has produced algorithms that are provably robust and achieve optimal statistical complexities. On the practical side, our algorithms are competitive with state-of-the-art deep learning methods on fastMRI data, with the added benefits of flexibility and modularity.
Action required
Problem: The current root path of this site is "baseurl ("_config.yml.
Solution: Please set the
baseurl in _config.yml to "Education
-
The University of Texas at AustinPh.D., Electrical and Computer Engineering2016 - 2022 -
IIT MadrasB.Tech.(with honors), Electrical Engineering2012 - 2016
Experience
-
UC BerkeleyPostdocJune 2022 - present -
IBM Research, Yorktown HeightsResearch InternMay - September 2019 -
Tata Institute of Fundamental Research (TIFR), MumbaiResearch InternMay - August 2015 -
Audience Communication Systems, BangaloreResearch InternMay - August 2014
News
Selected Publications (view all )
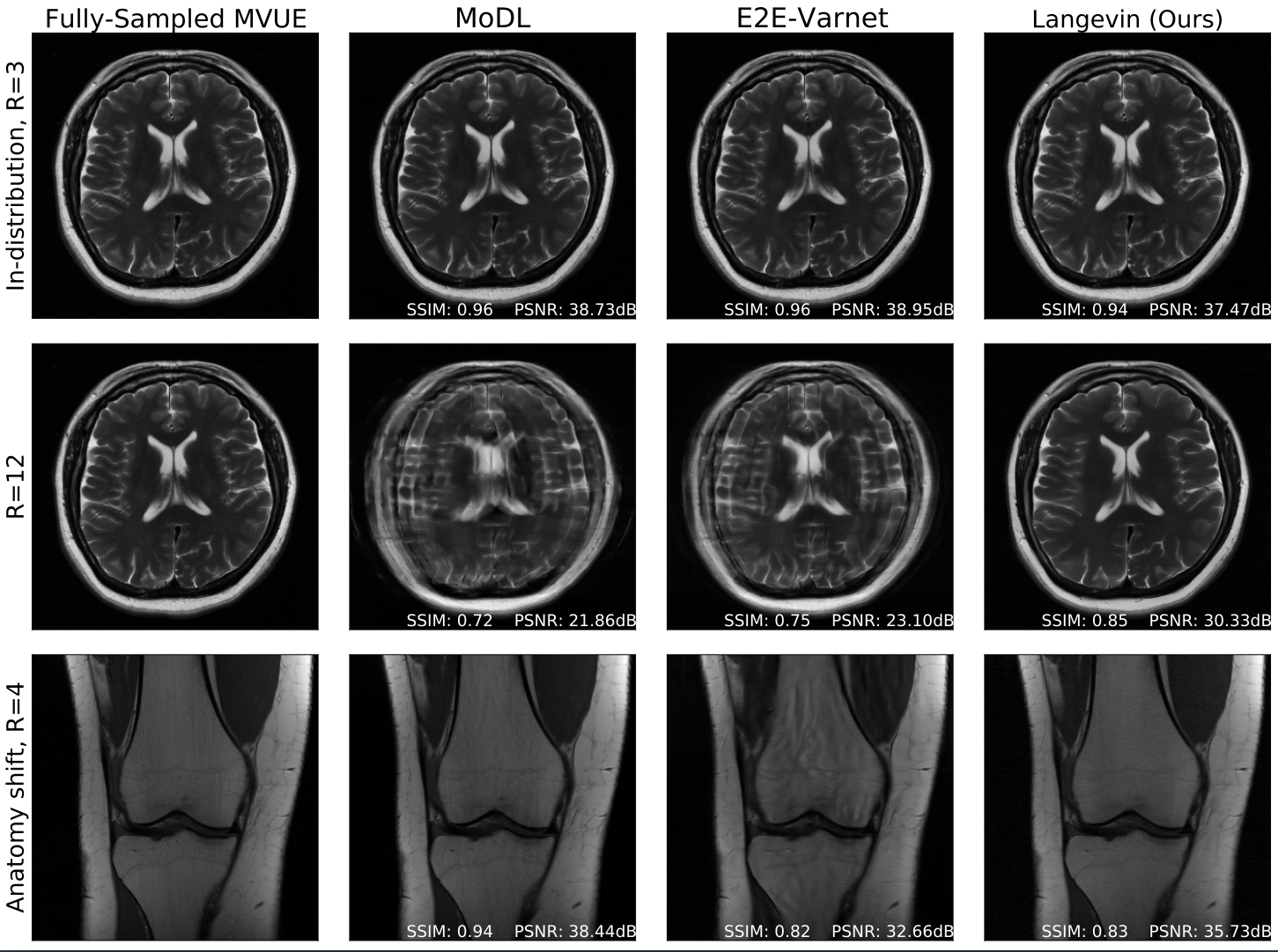
Robust compressed sensing MRI with deep generative priors
Ajil Jalal, Marius Arvinte, Giannis Daras, Eric Price, Alex Dimakis, Jon Tamir
Thirty-Fifth Conference on Neural Information Processing Systems (NeurIPS) 2021
The CSGM framework (Bora-Jalal-Price-Dimakis' 17) has shown that deep generative priors can be powerful tools for solving inverse problems. However, to date this framework has been empirically successful only on certain datasets (for example, human faces and MNIST digits), and it is known to perform poorly on out-of-distribution samples. In this paper, we present the first successful application of the CSGM framework on clinical MRI data. We train a generative prior on brain scans from the fastMRI dataset, and show that posterior sampling via Langevin dynamics achieves high quality reconstructions. Furthermore, our experiments and theory show that posterior sampling is robust to changes in the ground-truth distribution and measurement process.
Fairness for image generation with uncertain sensitive attributes
Ajil Jalal, Sushrut Karmalkar, Jessica Hoffmann, Alex Dimakis, Eric Price
International Conference on Machine Learning (ICML) 2021
This work tackles the issue of fairness in the context of generative procedures, such as image super-resolution, which entail different definitions from the standard classification setting. Moreover, while traditional group fairness definitions are typically defined with respect to specified protected groups–camouflaging the fact that these groupings are artificial and carry historical and political motivations–we emphasize that there are no ground truth identities. For instance, should South and East Asians be viewed as a single group or separate groups? Should we consider one race as a whole or further split by gender? Choosing which groups are valid and who belongs in them is an impossible dilemma and being “fair” with respect to Asians may require being “unfair” with respect to South Asians. This motivates the introduction of definitions that allow algorithms to be oblivious to the relevant groupings. We define several intuitive notions of group fairness and study their incompatibilities and trade-offs. We show that the natural extension of demographic parity is strongly dependent on the grouping, and impossible to achieve obliviously. On the other hand, the conceptually new definition we introduce, Conditional Proportional Representation, can be achieved obliviously through Posterior Sampling. Our experiments validate our theoretical results and achieve fair image reconstruction using state-of-the-art generative models.
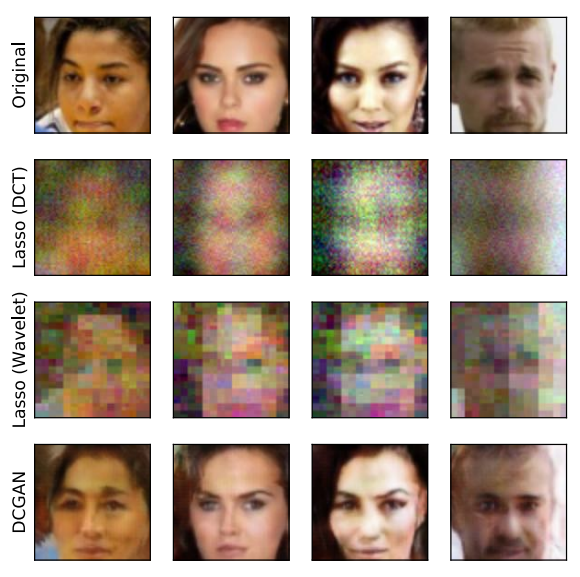
Compressed Sensing using Generative Models
Ashish Bora, Ajil Jalal, Eric Price, Alex Dimakis
International Conference on Machine Learning (ICML) 2017
The goal of compressed sensing is to estimate a vector from an underdetermined system of noisy linear measurements, by making use of prior knowledge on the structure of vectors in the relevant domain. For almost all results in this literature, the structure is represented by sparsity in a well-chosen basis. We show how to achieve guarantees similar to standard compressed sensing but without employing sparsity at all. Instead, we suppose that vectors lie near the range of a generative model $G : \mathbb{R}^k \to \mathbb{R}^n$. Our main theorem is that, if is $L$-Lipschitz, then roughly $O(k \log L)$ random Gaussian measurements suffice for an $\ell_2 /\ell_2$ recovery guarantee. We demonstrate our results using generative models from published variational autoencoder and generative adversarial networks. Our method can use 5-10 x fewer measurements than Lasso for the same accuracy.